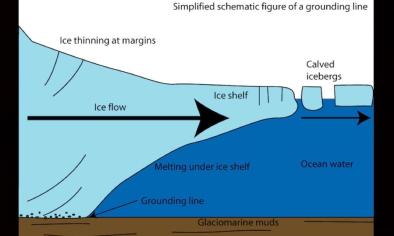
Hammering the Trend
Recent research from Oliva et al.[1] is all about trend change in temperature on the Antarctic Peninsula (AP). It follows in the footsteps of Turner et al., and their common conclusion is that since about 1998, the Antarctic peninsula — so often touted as one of the fastest-warming regions on earth — has been cooling, cooling even faster than it was warming before 1998.
...
What interests me is the statistics behind claims that the temperature trend changed. I’ll begin by putting some data together, combining the same 10 stations used by Oliva et al. I’ll align them in my usual way [using the pseudo-“Berkeley method”] and form a composite monthly average temperature anomaly for the AP as a whole.
Then I computed annual averages from the monthly averages. This really doesn’t lose any precision in trend estimates (somewhat counterintuitively), and greatly reduces the level of autocorrelation. Finally, I’ve got a time series — annual average surface air temperature — suitable for study.
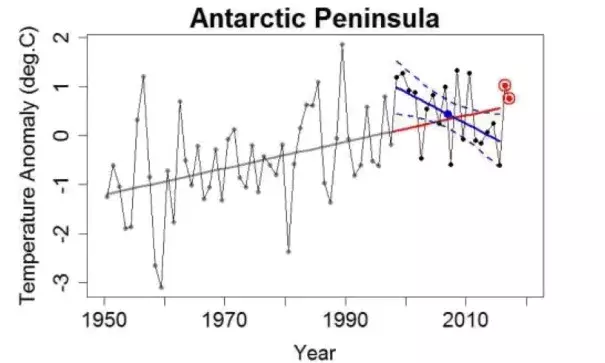
And I can see right away what Oliva et al. and Turner et al. are talking about. The estimated trend (by linear regression) from 1998 through 2015 is rather downward:

Using my combined data set, it’s cooling at 6.4 °C/century, faster even than reported by Oliva et al. and Turner et al. And with p-value equal to 0.03, we have confidence (97%, in fact) that the AP has been cooling over these 18 years.
And it surely doesn’t seem to be warming rapidly, in spite of the fact that it sure was prior to 1998:

Using that time period, the linear regression slope is upward at 2.7 °C/century, and the p-value of 0.007 leaves little doubt about its warming at 99.3% confidence.
Conclusion: the trend changed. With a 97% chance it’s now going downward, almost no chance it’s going upward as fast as it used to be going (back when we were 99.3% sure it was going upward), that’s some solid evidence. Hell, even tamino would admit it’s a trend change, right?
Let’s look closer.
The narrative is: warming fast through 1997, then cooling even faster since 1998. If the last 18 years is the change from warming to a rapid cooling trend, one would expect the 1998-2015 average to be less than it would have been, had that trend change not happened.
We can of course take the pre-existing (1950-through-1997 warming) trend and extrapolate it to the present, to see what would have happened (trend-wise at least) had no trend change occurred:

The big blue dot marks the 1998-through-2015 average of the observations. Notice that it’s above the value at that time for the extrapolated pre-existing trend (shown in red); just when it was supposed to be cooling so rapidly, its 18-year average went up, above expectation.
But that linear regression trend was 97% confidence downward? What’s going on? To get that result, you can’t just change the trend slope from warming to cooling, you also have to change the value of the trend line at 1998. But if you’re allowed to do that, there’s an extra degree of freedom (in the statistical sense) in how you’re modelling the data.
We all tend to ignore the “intercept” in a linear regression, and usually it really doesn’t matter. But when we have a model with two intercepts, we can’t just ignore them both. One of them represents a degree of freedom that won’t go away.
The right way to account for this is the Chow test, and when I apply it to the given data with a breakpoint at 1998, the p-value for a trend change becomes a paltry 0.061. It doesn’t even make 95% confidence, although it does make 93.9% confidence.
Well, at least it’s 93.9% confidence by some pretty strict standards. That’s not a “lock,” it’s hardly “fer sure,” but it’s likely enough that it deserves very serious attention, right?
Let’s look closer.
The breakpoint being tested is 1998. That’s fine if you have a reason to pick 1998. But if you picked it because it looks like there might be a trend change, based on the data you’re using to test for a trend change, then you’re cherry-picking. I often call it “innocent” or “naive” cherry-picking. You don’t need a nefarious purpose to look at 1998-2015 and think “Looks like a trend change … let’s estimate the trend starting then.” It’s natural.
But that means that when there’s nothing really going on, you still get all those previous years to start from and the chance that at least one of them will show signs of trend change is a lot higher than the chance a single random series will show such signs. It’s the fallacy of multiple trials — essentially, if you’re allowed to buy 100 lottery tickets you have a bigger chance of winning, but that doesn’t mean the lottery odds have changed.
When I run Monte Carlo simulations to compensate for the multiple trials, using a 66-year-long total record as I used for Antarctic (from 1950 through 2015), the “maybe impressive” p-value of 0.061 turned into a no-way-not-even-close p-value of 0.67. In other words, there’s about a 2/3 chance of finding a time span at least as suggestive as the one in the Antarctica data.
So no, I do not consider the evidence sufficient to regard cooling in the Antarctic Peninsula as being even likely, let alone established. It’s possible, and only time will tell, but the evidence presented so far isn’t strong enough to stand on its own.
Incidentally, since their studies there’s a little bit more data available, for 2016 and the first three months of 2017. Here’s an update of the previous graph, adding the 2016 and first-quarter-2017 values:
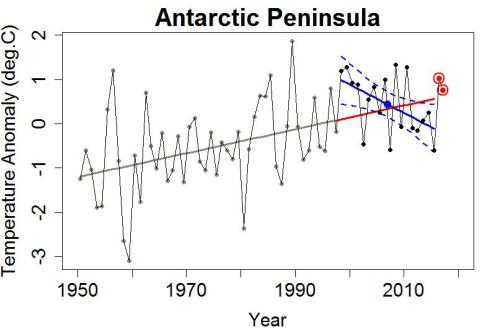
I note that 2016, and 2017-so-far, both came in above the trend line estimated from the pre-1998 data.
Related Content